简明控制理论:写在电磁悬挂国产化的2025年
PUBLIC自己本来算是计算机的背景,感谢这个教育让我有了一种“离散”的世界观。
后面做机器人,接触到很多控制背景的朋友,简单了解下发现这是一个和计算机相爱相杀的学科。
互相重复且独立地发明了不少相似的概念。更重要地,展示了一种“连续”的世界观。
这里简单记录一下控制里面比较核心的美妙观点。起码回答,什么是传递函数。
前置
不知道大家是不是和我一样都很久没用一些数学概念了,特别是连续函数里面的。
先提及几个概念:
所有的连续函数都是若干周期函数的加和
所以我们先关注某特定周期的函数:\(x = e^{st} = e^{\sigma t}\sin(\omega t)\)。
其中 \(s\) 是复数\(s=\sigma +i \omega\)。
一类微分方程的通解 \(\frac{d^2 y}{d t^n} + a_1 \frac{d y}{d t} + a_2 y = 0\)
先考虑 \(y=e^{st}\)。
所以就得到 \(s^2 e^{st} +a_1 s e^{st} + a_2 e^{st} = 0\),也就是 \(s^2 + a_1 s + a_2 = 0\),关于 \(s\) 的二元一次方程。
如果这个方程的解是 \(s_1,s_2\) 两个。
那么 \(y = e^{s_1 t}\) 和 \(y = e^{s_2 t}\) 是原方程的通解。
其任意线性组合也是: \(y = \sum_{k=1}^{2} C_k e^{s_k t}\)。
这里举例子是2次,次数更高的话也是一样。
归结为解一个高次方程的根的问题。(忽然想起来一直想写一个和伽罗瓦理论有关的,以后再说吧)。
这个对应的高次方程,被叫作 特征方程 。
开始刻画问题
从问题刻画开始,就是我陌生的领域了。
计算机用循环来刻画这个世界: \[x_{t} = a x_{t-1} + b u_{t}\]
经典控制里面用微分方程来刻画这个世界:
\[\frac{d^3 y}{dt^3} + a_1 \frac{d^2 y}{dt^2} + a_2 \frac{dy}{dt} + a_3 y= b_0 \frac{d^3 u}{dt^3} + b_1 \frac{d^2 u}{dt^2} + b_2 \frac{du}{dt} + b_3 u\]
举个具体的例子,如果 \(y\) 是位置, \(u\) 是推力,那么 \(\frac{d^2y}{dt^2} = u\),就是牛顿第二定律。
控制希望最终了解 \(y\) 的轨迹,是怎么被 \(u\) 驱动的。
那么我们来解方程。
系统的内在属性,方程的通解
我们先看看,如果没有 \(u\) ,\(y\) 自己会怎么变。
也就是 \(\frac{d^3 y}{dt^3} + a_1 \frac{d^2 y}{dt^2} + a_2 \frac{dy}{dt} + a_3 y = 0\) 的解。
上面讲过了,我们会得到:
- 假设 \(y = e^{st}\)
- 得到特征方程 \(s^3 + a_1 s^2 + a_2 s + a_3 = 0\)
- 得到一群 \(y = e^{s_kt}\) ,及其线性组合 \(y = \sum_{k=1}^3 C_k e^{s_k t}\)
这个就是这个系统的内在属性,比如我们谈到本体频率,一个桥,一个钟摆,在没有干预的时候,自己摇摆的频率。
注意这里每一个 \(s_k\) 都可能是复数,所以看几个例子:
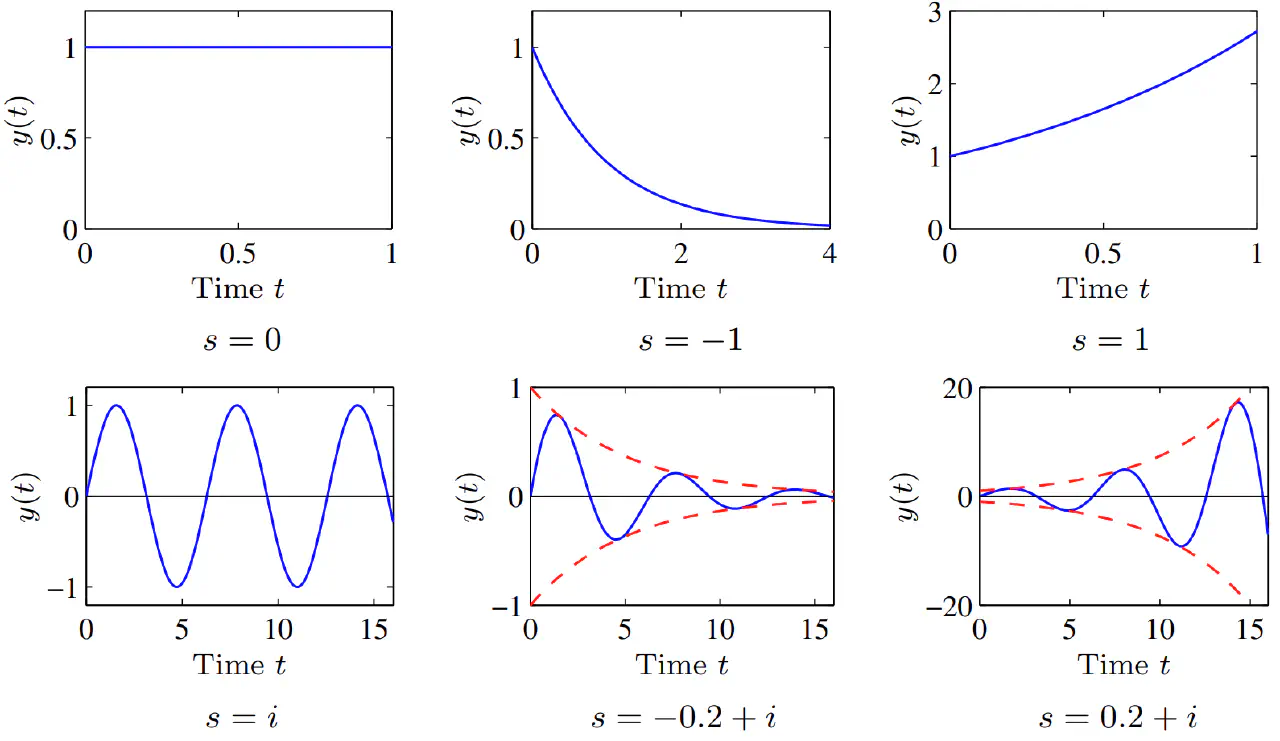
方程对输入的反应,方程的特解
接下来,我们看下在 \(u\) 存在的情况下,\(y\) 的轨迹怎么变。
特别的,我们先考虑一个周期输入: \(u = e^{st}\)。如果我们最后能得到一个 \(y=Xu\) 的关系该有多好,直接获得变换矩阵 \(X\)。
我们试着假设 \(y = G(s) e^{st}\),这里特别让 \(X = G(s)\) 是一个关于 \(s\) 的函数。
代入到一开始的方程里面,得到:
\begin{aligned} \frac{du}{dt} &= s e^{st}, &\quad \frac{d^2u}{dt^2} &= s^2 e^{st}, &\quad \frac{d^3u}{dt^3} &= s^3 e^{st}, \\ \frac{dy}{dt} &= s G(s) e^{st}, &\quad \frac{d^2y}{dt^2} &= s^2 G(s) e^{st}, &\quad \frac{d^3y}{dt^3} &= s^3 G(s) e^{st}. \end{aligned}
然后:\[(s^3 + a_1 s^2 + a_2 s + a_3)G(s)e^{st}= (b_0 s^3 + b_1 s^2 + b_2 s + b_3)e^{st}\]
也就是:\[G(s) = \frac{b_0 s^3 + b_1 s^2 + b_2 s + b_3}{s^3 + a_1 s^2 + a_2 s + a_3}\]
终于得到 传递函数 了。
到这里我们发现,传递函数是想找到一种简单的映射,直接把输入对系统的影响,叠加到系统的输出上去 \(y = Xu\)。
再加上我们前面的通解,总体来说,面对输入信号 \(u = e^{st}\),系统输出的轨迹是:
\[y = \sum_{k=1}^m C_k e^{s_k t} + G(s) e^{st}\]
悬挂
为什么是这个标题。
之前我想过一个问题:什么决定了一个车平稳,有没有像云台一样稳定的车。
我作为不懂车的人,感觉这个问题是网上营销的重灾区,现在一个简单的倾向是认为 空气悬挂 是好悬挂。
这不符合我的直觉,因为我觉得空气和弹簧都是弹性器件,性质应该几乎相同,只能解决,或者硬或者软的问题,但是不能像云台一样有“控制力”。
关键应该在于阻尼。然后发现了 电磁悬挂 技术,通过电流,改变阻尼器中液体的黏性,来主动调整阻尼。
合理,这个说法说服我了。今年似乎是专利过期了,后面应该会有很多用这种悬挂的车吧。
对了,他们叫作 磁流变悬挂 ,因为 电磁悬挂 已经在一些地方被CDC误用了,哈哈。(CDC是通过机械控制阻尼液的孔的大小来改变阻尼的一种方法)。
这几乎是一个spring–damper system:
\[m \ddot{y} + c(\dot{y} - \dot{u}) + k(y - u) = 0\]
其中:质量 \(m\),弹簧刚度 \(k\),阻尼系数 \(c\),路面输入 \(u\),车身高度输出 \(y\)。
得到传递函数: \[G(s)= \frac{c s + k}{m s^2 + c s + k}\]
如果 \(c\) 可以调整的话,这个系统应该会更有控制的可能性。
但是这里应该用什么控制律呢,今天我还不知道。