Music Theory: Building from the Scratch
PUBLIC如何用比较数学和推理的方法去理解和掌握音乐。
说一个有争议的话题,类似中医和西医。不分高下地做一个对比,西医更像是演绎法,中医更像是归纳法。
就像是how first principles thinking fails里面提到的inductive v.s. deductive。
不是说归纳法不好,而是演绎法可能更适合我这样的天赋不佳的人去理解。你跟我说,“感觉一下”,我太难理解了。
Building from the Scratch是模仿Linux From Scratch (LFS)。
第一章 从频率说起
声音
众所周知,声音是波。波有两个属性:频率 x 振幅。频率决定我们听起来声音的“高低”,振幅决定声音的“大小”。
声音是波,而不是粒子 :)。
所以声音存在“共振”现象。
也就是说,在自然界中,如果一个声音的频率是440Hz,往往440Hz的整数倍声音也会同时出现。比如880Hz(第2谐波),1320hz(第3谐波)等等。
为什么同样不跑调的人,有的人唱起来好听,有的人唱起来不好听。
就是因为每个人的谐波特性不同。
如果完全没有谐波,好不好听呢。
在电子电路出现之前,是很难产生单一频率的波的。但是现在我们可以用电路来实现非常单一的波,这种工具被称为合成器。构成了电子乐的基础。
音乐中的牛顿定律
上面我们说完了单一频率的波,接下来我们说如果多个频率连续出现,什么时候我们会觉得好听,什么时候会觉得难听呢。(这里的好听难听就无法形式化了,凭“感觉”)。
结论:
频率构成简单整数比的声音,放在一起听会比较好听。
比如:
- 上面提到,我们在发出440Hz的时候,880Hz的声音也同时存在,构成1:2的频率比,属于简单整数比。所以一个持续的单一音高,不会那么“难听”。
- 和弦是好听的,和弦是什么呢。和弦就是多个构成简单整数比的声音同时出现。比如我们最常见的C大三和弦,就是由频率比例是4:5:6的声音构成的。 在这里并不需要理解什么是C大三和弦。后面会再介绍。
到这里,我们提到“好听”很多次,我们的好听是基于我们身体机能的反应(可以再深究一下,但是不是今天)。
这里也应该形式化的表达一下人对声音的测量特性了。
- (大部分)人无法掌握的机能:听声音,就说出他的频率。
- (所有人)人可以听出来两个声音之间的频率比例。 我们把两个音的比例,给一个名字叫作 音程 ,声音之间的路程。最简单的音程就是1:2。
- 所以人的耳朵工作在Log尺度下。
下面,我们如果想构成一段声音的序列,我们该怎么选择频率呢。
比如我们先无脑选择440Hz(这个440Hz完全是人为定义,历史惯性,完全可以改成别的),那么我们可以先想到880Hz,这个没问题,听起来是“和谐”的(后面我们会更多用和谐来指代好听)。
然后我可以选择440Hz的1/2,1/3,1/4…1/13,每个音给一个键,用合成器来开始演奏了。
这样可以吗,其实是可以的,但是历史的车轮走到今天,我们现存的音乐体系里面用的是1234567,七个音。也就是说,在1:2的整个音程[440,880]里面,切分出来7个音。
为什么是7个音
我们进入第一个真正有意思的环节了。
为什么是7个音呢。历史上是怎么发生的?
首先,我们看看哪些整数比是好用的,1:2两倍频率,没有问题。2:3也是很整的。
2:3是如此之好听,那么让我们重复它
f = 440
for i in range(13):
print(i,f)
f = f * 3/2
if f > 880: f=f/2.0
0 440
1 660.0
2 495.0
3 742.5
4 556.875
5 835.3125
6 626.484375
7 469.86328125
一直循环到第7个,我们似乎又回到了原点,469和440很接近了,那么我们停下来吧。
一个小小的修复
在上面的过程之后,我们得到了8个音符(下图中灰色+红色,重色是上面迭代中的(7,469)。 但是,我们遗憾地发现3:4这个良好的整数比竟然没有用上(下图中蓝色)。
所以,决定,把红色换成蓝色。最终得到7个音符。
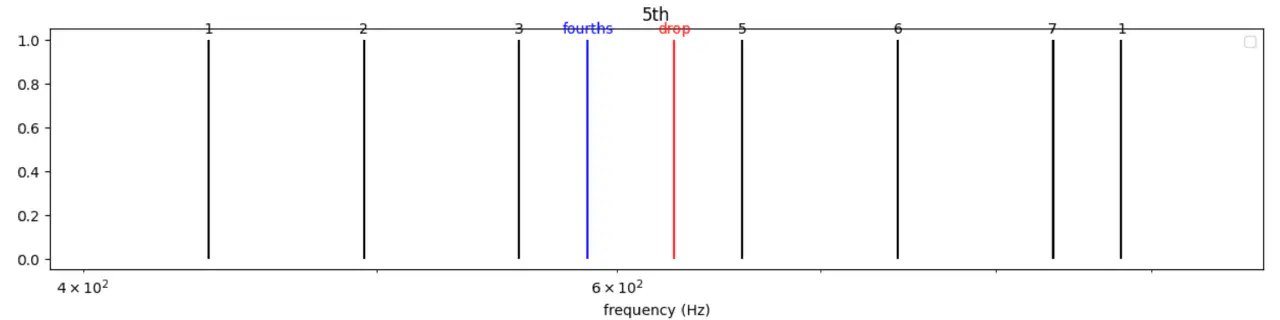
这种方法又被称作五度相生律,据说是毕达哥拉斯学派发明的。
形式化的开始,巴赫十二平均律
在上面的五度相生律之后,要过了很长很长一段时间,人们才真正学会log/exp算符。(巴赫会不会啊,不知道)。
所以被大佬巴赫,重新发明了十二平均律:假如我们需要一个步长\(s\),使得连续走 \(12\) 次,走出一个 \(2\) 倍音高,也就是\[s^{12}=2\] 或者说 \[12 \times \log(s) = \log(2)\]
上面的结果,如果我们用现在我们掌握的exp来操作,并且去增加划分:
t=12
octaves = [440*(2**i) for i in range(2)]
fifth = [octaves[i] * 3/2 for i in range(1)]
fourths = [octaves[i] * 4/3 for i in range(1)]
new_notes = [octaves[0] * (2**(float(i)/float(t))) for i in range(1, t+1)]
plot(f"{t} divisions (notes)", [(octaves, 'k', "octaves"), (fifth, 'r', "fifths"),(fourths,'b', "fourths"),(new_notes,'g', "new notes")], 'log')
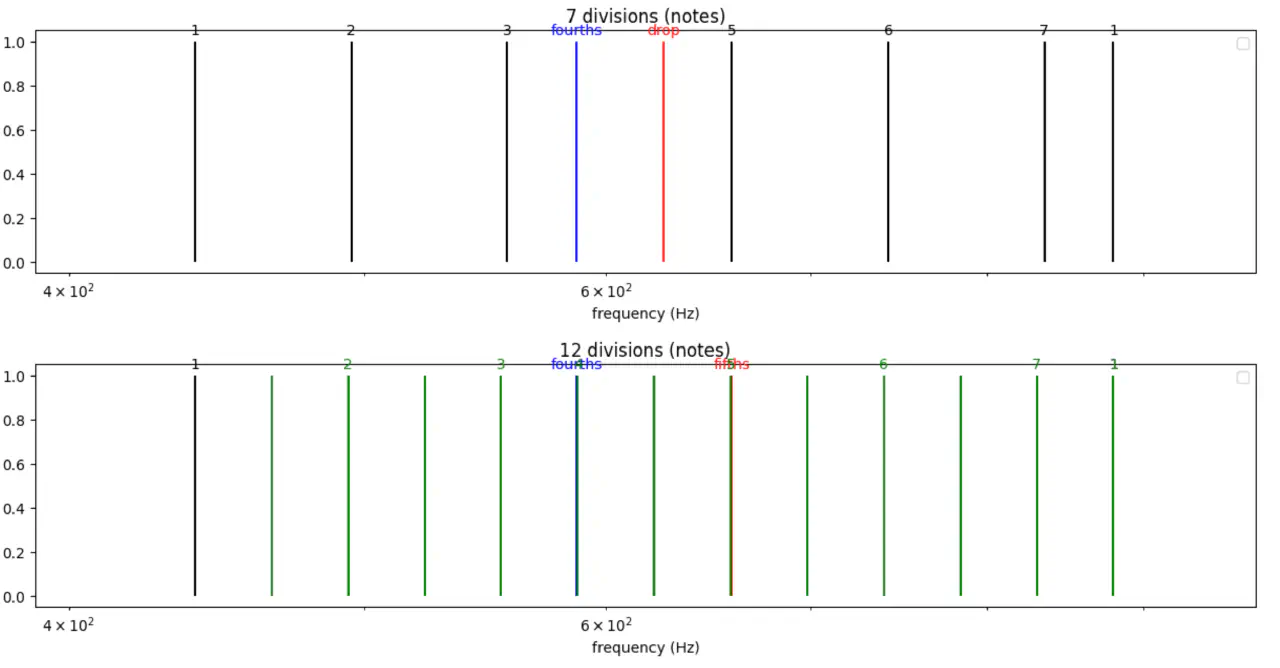
我们就直接得到了12个划分,并且:
- 充分利用了1:2 2:3 3:4这三个良好的整数比。
- 尊重了传统,上面的7个音符也都被覆盖了,历史上的曲子不用重写了。
这里,我们有了新的观察,原来1-2之间和3-4之间,不一同样的“距离”。
- 3-4和7-1之间距离比较小,在十二划分里面,这两个之间的距离是一个单位,被叫作一个 半音 。
- 其他音之间的距离比较大,是两个单位,被叫作一个 全音 。
到了这里,终于有一个比较“良好”的数学表示了。
我想起来小时候上音乐课,有一种题算是简谱的完形填空,给你一个旋律,盖住其中一个音符来猜答案,当时我很想用类似等差数列之类的东西去找答案。
现在看来,当时猜的成绩如此之差也可以理解了。音阶竟然不是连续的。
用流行的话说,12平均律给出了一个最基础的latent representation。
数学上的不严谨性
上面两种方法,五度相生律和十二平均律找到的音符,从数学上不是完全相等的。
十二平均律找到的都是无理数,原本的五度相生律找到的都是有理数。
这是一个细节。
十二平均律确实更加整齐,也有很多优点,但是五度相生律更接近最基础的整数比定理。
所以严格来说,十二平均律是方便,但是不够好听或者说和谐的那一个。
除了这两个之外,还有一些其他的律。甚至这也算一个专门的领域:律学。
第二章 旋律和和弦的关系
和弦出现了
这样,和弦就出现了,几个音放在一起听,比较和谐,他们就算是一个和弦。
二(个音的)和弦
比如1-5,如果大家还记得话,他们是2:3的关系,听起来很好,同理2-6也听起来很好。而且1-5和2-6听起来会有点像。
三(个音的)和弦
再多一个音的话,1-3-5的比例是4:5:6,这个就有点高级了,它是由1-3的4:5和1-5的2:3组成的。
另外一种理解是,它是由1-3这个音程和2-5这个音程组成的。根据十二平均律,1-3是4个半音的音程,3-5是3个半音的音程。 先走4步,再走3步。
继续往下平移呢,2-4-6,他是由2-4和4-6组成的,其中2-4是3个半音,4-6是4个半音。 先走3步,再走两步。
和弦就是上面最基础的representation之上一点,更常用的一种representation。
而和弦之中,三和弦占据了主导地位。
三和弦中,1-3-5(4步+3步)和2-4-6(3步+4步)被人们听出来最容易区分,他们的性格(从听感来说)最容易区分。
所以人们给了他们一个非常朴素的名字,4+3是大(三)和弦,3+4是小(三)和弦。
旋律的基础:离家出走->归来和解
在斯多葛主义(Stoicism)中提到,快乐无法脱离痛苦而存在。这个说法在旋律中隐隐地体现出来。
旋律,可以被认为,从完美的和谐出发,走出一些不和谐,最终回到和谐的过程。
是不是有点像自虐狂。
或者像走钢丝绳,微微失去平衡,再回来。这种过程,构成了旋律。
可以把音符想象成一个序列,每次产生一个新的音符的时候,我们要考虑两个因素:
- 希望下一个音符和之前的音符连续出现比较和谐,贴近和弦
- 是不是该回家了,回到最初的音。不妨假设,我们是从1出发,那么最终我们都是要回到1的。
这就是旋律,从家出发,最终回到家,这期间的探险经历,就是旋律。有的旋律明亮昂扬,有的旋律忧郁灰暗,只是在每一步的选择不同。
第三章 旋律的色彩
十二平均律的预测性
历史发展起来,发现了一个物理规律,这个规律一方面可以解释过去的现象,更重要的,应该可以预测未来。
现在我们有了:12个划分,12个音符。我们先用下标来指代他们。我们目前最常用的音符,还是用五度相生律做出来的,也就是[0, 2, 4, 5, 7, 9, 11, 12/0]。
我们也慢慢意识到,声音的一切都是围绕相对的音程概念的,绝对值不是那么重要。
所以我们有两个猜想:
- 能不能平移。 比如[2, 4, 6, 7, 9, 11, 13, 14] 。答案是可以的。而且对大多数人来说,在不做A/B对比的情况下,两种方法演奏的歌听起来是一样的, 在上面的[0,2..12]和[2,4..14]里面,不变的是音和音之间的关系,都是 全全半全全全半 。
- 能不能换家。 比如[9, 11, 0, 2, 4, 5, 7, 9]。答案也是可以的,但是这种替换,听起来就不一样了。这次变换之后,音和音之间的关系变成了, 全半全全半全全 。
一种变换不影响听感,这个好理解。一种变换影响听感,也好理解。
一切都是因为音程的组合不同。
第一种变换,更多的作用在于更改旋律的高低,去做乐器之间的配合。
其实主要是配合最不稳定的一个乐器,就是人的嗓子。
人的嗓子的一致性很差,不同的人能唱的高低音差别很大,特别是男女之间的差异也比较大。
第二种变换更具延伸性。如果我们不想改变音符,是不是可以多做一些变换:
- 12345671
- 23456712
- 34567123
- 45671234
- 56712345
- 67123456
- 71234567
到这里,我有点不可思议了,原来怎么搞都行啊。
确实是怎么搞都行,但是有的好听,有的不好听。或者说有的更大众,更多人听起来舒服,有的更小众,只有乐于挑战的人愿意去尝试。
大调小调
在7个变换中,最常用的,也就是说在没有理论指导的情况下,大家试错出来的,最不难听的。是第一个和第六个。
第一个被叫作, 大调音阶 。第六个被叫作, 小调音阶 。
人们用一个调式里面的第一个三和弦来简化称呼这一个调式。
大调音阶的第一个三和弦是1-3-5,上面说过,这是个大三和弦。
小调音阶的第一个三和弦是6-1-3,上面说过,这是个小三和弦。
中古调式
其他的也都有名字,而且个顶个的名字非常高大上。
| 1234567 | Ionian Mode | 伊奥尼亚调式 | 大调音阶 |
| 2345671 | Dorian Mode | 多利亚调式 | |
| 3456712 | Phrygian Mode | 弗利几亚调式 | |
| 4567123 | Lydian Mode | 利底亚调式 | |
| 5671234 | Mixolydian Mode | 混合利底亚调式 | |
| 6712345 | Aeolian Mode | 艾奥利亚调式 | 小调音阶 |
| 7123456 | Locrian Mode | 洛克利亚调式 |
中古调式的中古,意思是中世纪。中古调式又叫作教堂调式,意思是中世纪的罗马教堂发明的。
教堂为了影响大家,发明了很多东西。
曾经去过一些欧洲的著名教堂,进去之后,看着那些高高的穹顶,看着精美的雕像和壁画,听着教堂音乐以及被刻意设计的房间混响。 有一种我也想加入的感觉,对人的影响力真的很强。
建筑和音乐很多的起源就是宗教的传播需求了。
中古调式有点太复杂了。
但是我们平常听的音乐应该99%都是大调或者小调。
其他的调式就好像钢丝绳上的高难度动作,不容易玩好,玩好了也难免曲高和寡。
两个应用
中国调式:宫、商、角、徵、羽
中国的宫商角徵羽算是什么调式呢。首先他音符不够啊,他只有5个。
实际上他是123561。就是去掉了4和7。
这两个被去掉,一点也不怨,他们都太不独立了,4和3只有一个半音,7和1之间也只有一个半音。
去掉之后,剩下5个音符。从这5个音符里面任意选择音去构成二和弦或者三和弦,概率上来说,更容易和谐了。
摇滚五声音阶
这个也是经常被提到的一个名字。
玩摇滚的为了简化技巧,强化情绪,也去掉了两个音符。
他们选择的是61235。基于同样的原因,我们去掉了4和7。
总结来说,中国调式是5音符的大调,摇滚五声音阶是5音符的小调。
如果手边有什么乐器可以弹一弹的话,会发现这几个音符,随便弹,其实都不算难听。这不就是即兴了嘛。
结尾
写这些内容,诚惶诚恐,因为我自己是一个半吊子。
但是还是被write_it_down和let’s_have_a_talk鼓励,写一些,帮助自己厘清思路,也看看能不能结交新的朋友讨论讨论。
好读书,不求甚解;每有会意,便欣然忘食。