双目相机的观测距离是怎么算出来的:Probabilistic Programming
PUBLIC我们都知道贝叶斯定理,也知道围绕这个定理的一些反直觉的故事:比如在一定的假设下,去医院即使检测出疾病,也是不得病的概率更大。
但是我们没有一个很好用的工具,回答一系列这样的问题:在设定一些假设并经历一系列事件后,哪个结果出现的概率更高?
从计算机的角度看,我们缺少一个可以操作概率分布的工具库。
当然,这样一个轮子已经被发明了。
介绍一个我觉得很实用,但是并不常听说的编程工具:Probabilistic Programming Language
贝叶斯定理101:癌症测试
我们有以下假设:
- P(Cancer) = 1% 人群中有1%的人有癌症
- P(Positive | Cancer) = 80% 如果有癌症,我们现在的检测手段可以以80%的概率检测出来
- P(Positive | No Cancer) = 9.6% 如果没有癌症,也有9.6%的概率误报
- 我们想知道 P(Cancer | Positive),也就是在检测结果为阳性的情况下,患癌的概率是多少。
先说答案:即使检测出癌症,真实得癌症的概率是7.76%
贝叶斯定理: \[ P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)} \] 我们有
\[ P(\text{Cancer} \mid \text{Positive}) = \frac{P(\text{Positive} \mid \text{Cancer}) \cdot P(\text{Cancer})}{P(\text{Positive})} \]
接下来的变换用到了全概率公式。
\[ P(\text{Positive}) = P(\text{Positive} \mid \text{Cancer}) \cdot P(\text{Cancer}) + P(\text{Positive} \mid \text{No Cancer}) \cdot P(\text{No Cancer}) \]
\[ = (0.80 \times 0.01) + (0.096 \times 0.99) \]
\[ = 0.008 + 0.09504 = 0.10304 \]
应用贝叶斯定理
\[ P(\text{Cancer} \mid \text{Positive}) = \frac{0.80 \times 0.01}{0.10304} = \frac{0.008}{0.10304} \approx 0.0776 \]
结论
\[ P(\text{Cancer} \mid \text{Positive}) \approx 7.76\% \]
import jax.numpy as jnp
from jax import random
import numpyro
import numpyro.distributions as dist
from numpyro.infer import MCMC, DiscreteHMCGibbs, NUTS
def mammogram_model():
has_cancer = numpyro.sample("has_cancer",dist.Bernoulli(0.01))
prob_positive = jnp.where(has_cancer, 0.80, 0.096)
numpyro.sample("test_result", dist.Bernoulli(prob_positive), obs=1)
# Use DiscreteHMCGibbs with NUTS
kernel = DiscreteHMCGibbs(NUTS(mammogram_model))
mcmc = MCMC(kernel, num_warmup=5000, num_samples=20000)
mcmc.run(random.PRNGKey(0))
samples = mcmc.get_samples()
posterior = jnp.mean(samples["has_cancer"])
print(f"P(Cancer | Positive) ≈ {posterior:.4f} ({posterior * 100:.2f}%)")
输出:
sample: 100%|██████████| 25000/25000 [00:16<00:00, 1513.40it/s, 1 steps of size 3.40e+38. acc. prob=1.00]
P(Cancer | Positive) ≈ 0.0786 (7.86%)
结果对了,但是不是准确的,因为整个方法是基于采样的。
真实的例子:如何分析一个双目相机的测距精度
在机器人中,经常使用双目相机来做双目观测。
一个常见的问题是:拿到一个相机,我们该如何分析它的观测精度?
首先我们需要了解双目测距的原理:
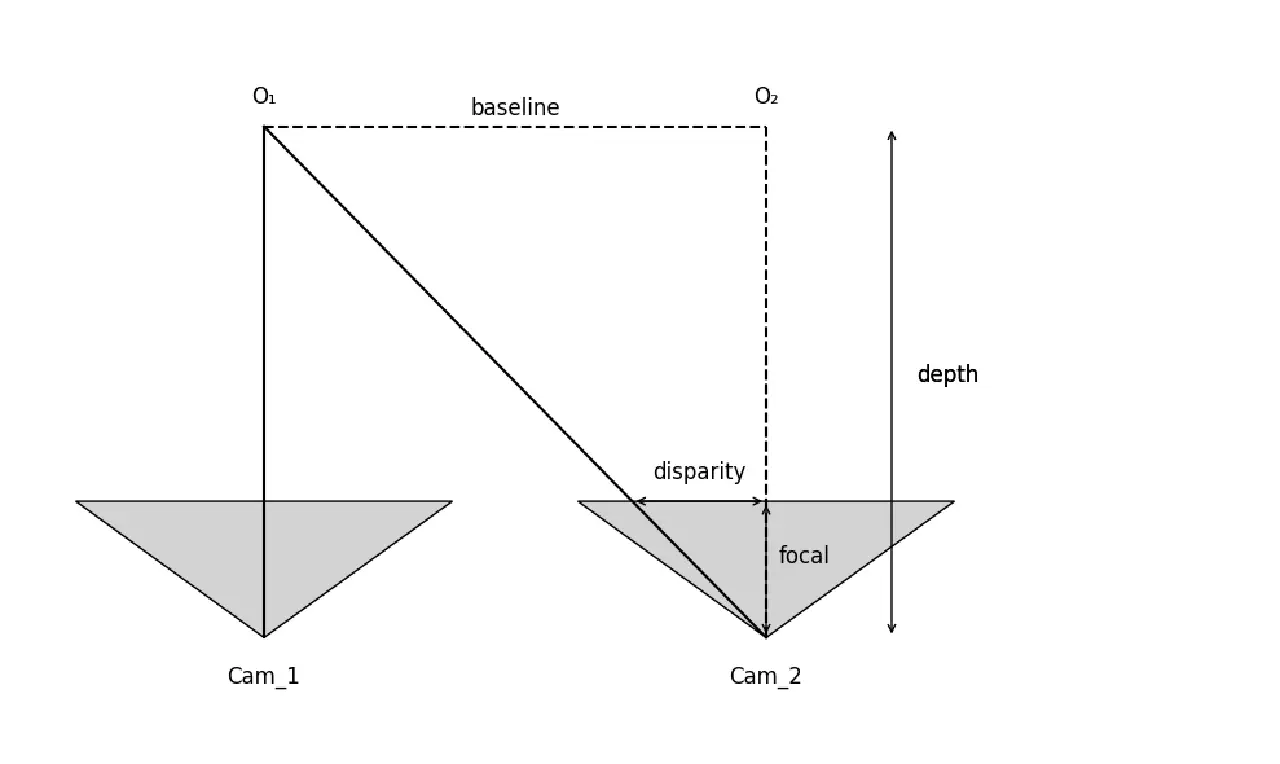
用图中O_1, O_2, Cam_2的三角形和他的相似三角形,\(\frac{\text{disparity}}{\text{focal}} = \frac{\text{baseline}}{\text{depth}}\), 也就是 \(\text{depth} = \frac{\text{baseline} \times \text{focal} }{\text{disparity}}\)。
所以,我们有几个观察:
- 最重要的,距离和视差是倒数关系,时差越小,距离越远。而且不是线性的。
- baseline 越大,测量的最大距离越远”
- focal越大看得越远,对应FOV越小
所以,为了方便,我们将视差为1像素时对应的深度称为“观测距离”。
比如一个相机是VGA分辨率640x480,FOV是90度,这两个参数粗略可以算出Focal Length是320。
baseline在5cm的情况下,观测距离是\(\frac{0.05m \times * 320px}{1px}=16m\)
然后,我的观测误差是多少呢。
我们还缺一个条件:disparity(视差)是如何定义的。
由于 disparity 是通过算法估算得出的,无法直接精确定义,只能通过实验拟合。
比如,我们先认为,他是一个均值是0,方差是0.3像素的高斯分布。
import jax.numpy as jnp
from jax import random
import numpyro
import numpyro.distributions as dist
from numpyro.infer import MCMC, NUTS, Predictive
import matplotlib.pyplot as plt
# Known constants
baseline = 0.05 # meters
focal_length = 320.0 # pixels
# Define the model
def depth_model():
disparity = numpyro.sample("disparity", dist.Normal(1, 0.3))
depth = (baseline * focal_length) / disparity
numpyro.deterministic("depth", depth)
# Run inference with prior predictive sampling
rng_key = random.PRNGKey(0)
predictive = Predictive(depth_model, num_samples=3000)
depth_samples = predictive(rng_key)['depth']
# Compute the mean
mean_depth = jnp.mean(depth_samples)
std_depth = float(jnp.std(depth_samples))
# Plot histogram
plt.hist(depth_samples, density=True, color='skyblue', bins="auto")
plt.axvline(mean_depth, color='red', linestyle='dashed', linewidth=2, label=f'Mean = {mean_depth:.2f}, Std = {std_depth:.2f}')
# Add labels and title
plt.xlabel("Depth (Z)")
plt.ylabel("Density")
plt.title("Depth Distribution (from Gaussian disparity)")
plt.grid(True)
plt.xlim(5, 50)
plt.legend()
plt.show()
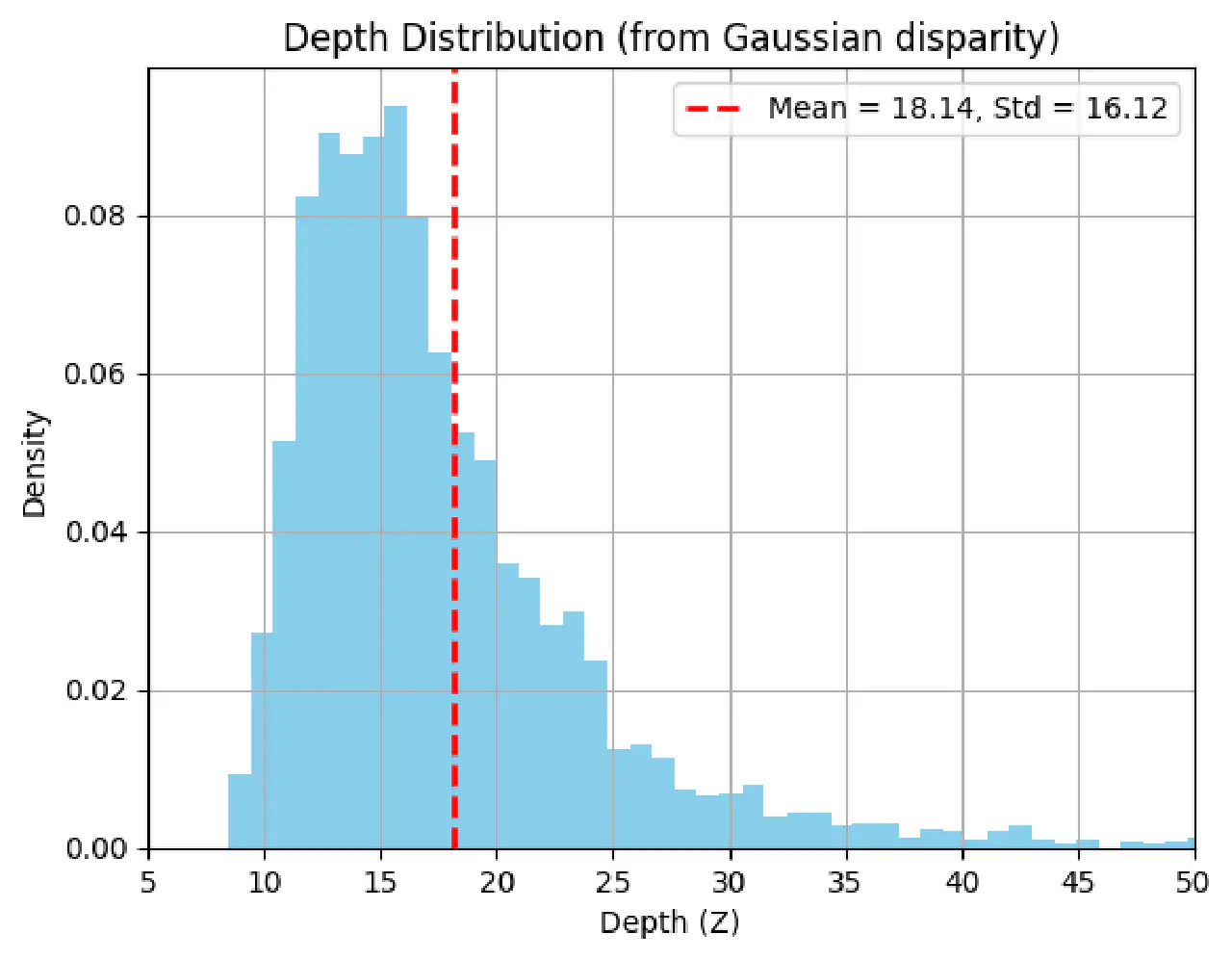
有趣的结果:
- 不是一个高斯分布,这是合理的。因为倒数不是一个线性运算,不会保持高斯分布。
- 均值不是在16m处。
- 得到的depth的标准差相当大,有16m
- 这里插一句,如果不用采样的方法,我们通常会把depth_model线性展开,得到一个线性模型,然后我们就认为不管怎么传递,都能保留高斯分布。用这种方法算出来的结果是\(\mathcal{N}(16, 15.18^2)\)。
一个小工具
Depth: -- m
告别高斯分布
正如用MBTI来定义一个人是片面的,仅用均值和方差来描述一个分布也同样过于简化。
PPL给了我们一个方便的方法去查看不同类似的分布。
比如,有一些我很喜欢的结果:
在visual localization中,用远处的点好不好呢?
结果是,远处的点会对旋转更有帮助,但是对位移没有帮助。
这也解释了我之前在做双目自标定时候的一个发现:无穷远处的点对于旋转标定的精度至关重要。
越来越多的数据对结果的提高是什么关系呢?比如SLAM中用的特征点数量。
我们直觉上知道,应该不是线性关系。
理论和PPL的实验都说明是一个开方关系,也就是说,数据量提升 100 倍,标准差大约能降低 10 倍。
一个slam的例子:https://taku-y.github.io/notebook/20170919/slam_advi.html
不要幻想了,没法实时的
这么好的东西。如果万物都自带一个分布描述,这个世界该有多美好。
但是这套方法的主要基础,是类似Gibbs sampling的一套东西,和往地上投针估计PI没什么区别。
所以也谈不上效率和实时了,离线玩一玩还是可以的。